As one who primarily studied mathematics in school, yet strives to maintain a philosophical habit of mind with pursuits like The Broken Binnacle, I often feel as though my time spent on pure mathematics requires justification. One perception I encounter is that math is simply a weird thing to choose to focus on: what kind of depraved self-loathing could lead one to voluntarily study analysis? The other common perception is that it seems like just a nice thing to have the skills to apply when the occasion arises; but then why not study physics or some kind of applied math?
Our culture has a “love-hate” relationship with mathematics. We love its uses and benefits, and cannot imagine life without the results of every discipline from geometry to calculus and beyond. But most only learn the world-altering results of these disciplines with much confusion, wasted effort, and frustration along the way. This problem is easy to blame on the modern methods of mathematical instruction, and I would recommend reading this article in ClassicalEd Review on this topic. To build on the points made therein, I propose that the shift away from the use and study of algorithms is largely to blame for our widespread misunderstanding of what pure mathematics actually is and what would lead one to study it. And this is where I would like to begin this defense of pure math.
Initially, we should observe that there are different “levels,” so to speak, of mathematical problems. The first level can be characterized by the representative equation 2+2=4. l will refer to this class of problems as “first-order mathematics” since such questions exist at the first level of mathematical abstraction (i.e., abstraction of specific physical quantities, expressed numerically). This is where most modern mathematical education focuses, and problems of this sort are solved with a numerical answer; you show your work, then circle the solution, and you are done.
The article in the Classical Ed Review hints at the second level of mathematics, characterized by the study of algorithms. Rather than reasoning about abstractions of specific quantities, this second order mathematical reasoning is a result of pattern recognition which allows one to conceptualize 2+2=4 at a higher level of abstraction such as a + b = c, and a + a = 2a. The ambition of this sort of thinking is that we can create a method, called an algorithm, to solve all first-order problems of a given class or type. This level of mathematical thought, while much more powerful than first order, is nevertheless more teachable, because unlike the first order, it is operating at the same level as our language. We use the same word, “addition” to refer to entire classes of first order problems precisely because there is a common process that we observe that transcends the specific quantities being added. We don't really “learn” the sum of every possible pair of numbers; we learn how to add.
So why does modern mathematical education seem to stunt the growth of its pupils by fencing them into first-order thought? The most charitable answer is that progressive teachers are seeking to promote a deeper understanding of what the arithmetic operations do practically, and why they work, by keeping the students tethered to the physical realities that underlie mathematical abstraction. This is an understandable response to the students who cannot help but question “why?” in their math class. Too often, the response to such questions is dismissive: “it just is that way.” Providing a more robust response to the skeptic inside every child is a noble intention, to be sure, but the method of demonizing abstraction and favoring the particular is terribly misguided.
Rather than looking back to the physical source of the original mathematical abstraction for definitions and causal explanations of mathematical operations, we must ascend further up the ladder of abstraction to the third order of mathematical thought. We arrive at this level by examining why the algorithms of the second level work through the use of proofs from axioms and definitions. Sometimes, as in the case of addition, we find that the algorithms are definitional themselves, once restated in terms that are axiomatic or at least logically prior to mathematics. The existence of some unit, denoted “1,” is axiomatic to the mathematician; of course, it is in fact the conclusion of the higher science of metaphysics that essences and natures exist as a unitive, i.e., indivisible, principle of substances. But—and this is the root of mathematical formalism—the content of “1” is immaterial to the mathematician, and the addition of 1 to itself in an iterative way is actually the definition of the natural numbers (yes, funnily enough, the term “natural numbers” refers to their derivation from natures, the metaphysical principle that most moderns reject). So, in cases such as these, an examination of algorithms leads us to ponder metamathematical questions that point us toward even higher sciences.
Other times, as in the case of Euclid’s algorithm to find the greatest common divisor of two integers, the examination of why the algorithm works presents a deeper observation about the nature of the underlying structures themselves, and so one begins to study those structures on their own terms. Studying the order of mathematical objects, qua order, is the essence of third level mathematical thought (an example of this would be a comparison between the structure of the integers, which is called a ring, and that of the rational numbers, which is called a field). Most students who stop their mathematical journeys after a semester of calculus likely have little to no practice in this type of mathematics, but the study of Euclid is a common starting point for those looking to explore it. The axiomatic approach pioneered by Euclid stems from a desire to completely grasp the causes and definitions behind the methods and observations already well documented and evidenced through years, and even generations, of practice and experimentation. It is shameful though, that our current model for teaching math leaves out the requisite study of the axioms and fundamental proofs that underlie algebra, and even basic arithmetic!
At this point, though, we may meet the objection that the study of the axiomatic structure that underlies basic arithmetic is more confusing than helpful, and that it could cause many students to actually regress in their understanding from a position of clarity and fluency to one of inefficiency and obscurity. Perhaps it would be demoralizing to have to go back as a junior high student and examine under what circumstances a (b + c) = ab + ac = (b + c) a is true. But it would certainly be eye-opening to realize there are whole branches of mathematics built around real systems in which it is not true. Doing these and other seemingly trivial proofs is actually a necessary step on the path to truly comprehending the meaning of even the most basic mathematical structures.
These pursuits of third-order mathematics are admittedly quite abstract and often seem irrelevant. But even grade schoolers seem to have a skeptic inside of them when they learn the algorithms of arithmetic and ask questions like, “what if we find a case where the long division algorithm is wrong, or where unique prime factorization isn’t true?” However, even if the satisfaction of the inner skeptic is not sufficient reason to convince us to embark on this pursuit, the primary benefits of this study go far beyond the proof of the mundane and the “obvious.” But that will be the topic of my next essay.



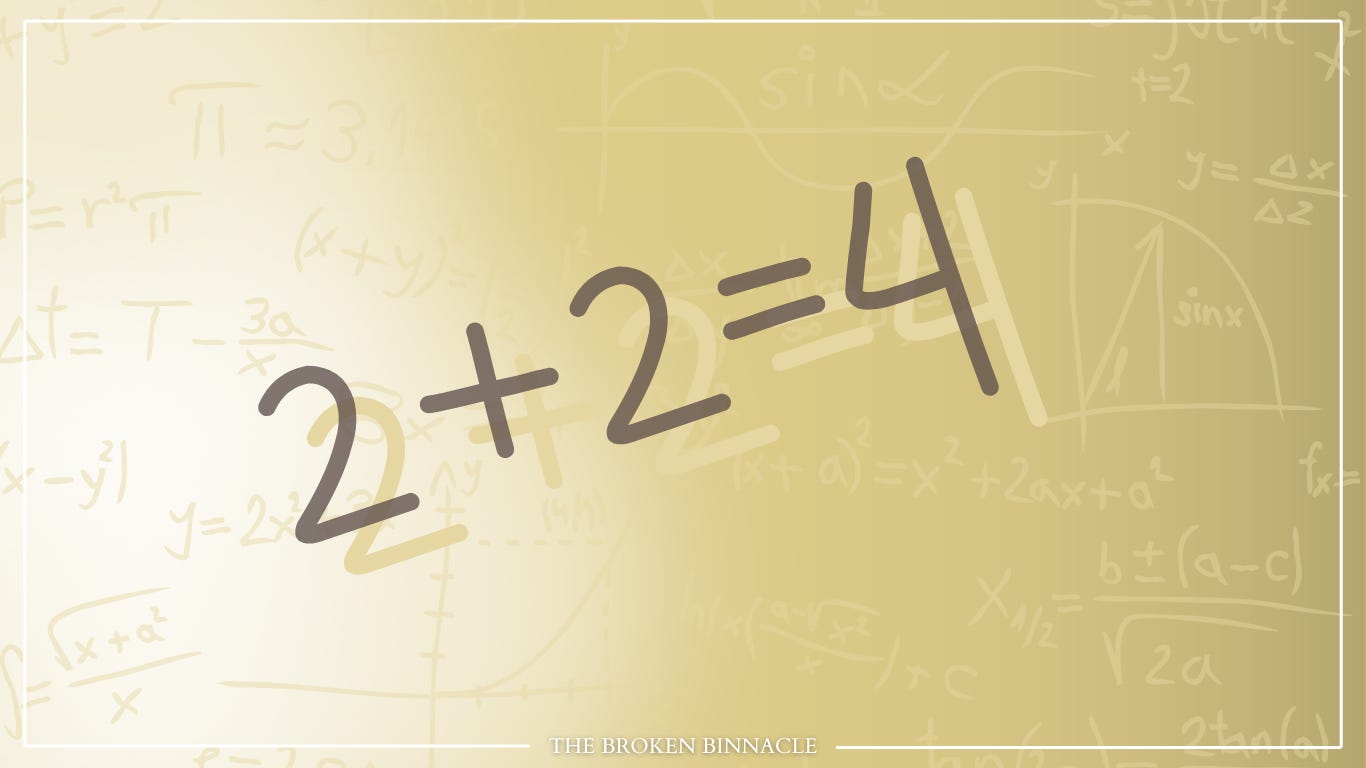
I study mathematics as a primary occupation and spend the remaining time reading and discussing History and Philosophy. Every single person I talk to, I have to explain the purpose of the things I do: with colleagues, I have to justify the study of "dead men stories and dead men thoughts"; with friends, I have to justify the study of "tortuous head-hammering"